O que são juros compostos e como funcionam nos teus investimentos

Se está a dar os primeiros passos no mundo do investimento — ou, pelo menos, decidiu finalmente fazer algo com o seu dinheiro — há um conceito fundamental que todo o aforrador informado deve conhecer: o juro composto.

Graças aos juros compostos, os investimentos de longo prazo tornam-se uma estratégia bastante atrativa para, ao longo do tempo, construir um património que funcione como uma almofada financeira no futuro.

Se ainda não está familiarizado com o conceito de juros compostos no contexto dos investimentos, explicamos neste artigo o que são e como se calculam.

O que são os juros compostos?

Os juros compostos são calculados com base no capital inicial e incluem todos os juros acumulados dos períodos anteriores. Isto significa que os juros são somados ao capital, e, no período seguinte, o cálculo dos juros incide sobre o novo montante total. Este mecanismo permite que os investimentos cresçam a um ritmo progressivamente mais acelerado com o passar do tempo.

Assim, os juros compostos surgem sempre que o juro é adicionado mais do que uma vez por ano, ou se for acumulável e reinvestido — como acontece, por exemplo, em capitalizações mensais.
Este tipo de capitalização é muito comum em finanças e economia, e constitui frequentemente a base das estratégias de investimento de longo prazo, como o value investing.

Ao investir, é importante compreender o extraordinário potencial dos juros compostos, pois este pode ser determinante para o sucesso a longo prazo. Devido ao impacto significativo que pode gerar ao longo do tempo, é frequente vermos referências ao conceito como “a magia dos juros compostos”.

De facto, há um mito que conta que, certa vez, perguntaram a Albert Einstein qual era a força mais poderosa do universo, ao que ele terá respondido: “Os juros compostos.”

Características do juro composto

O segredo dos juros compostos assenta em dois princípios simples: tempo e reinvestimento dos juros.
Ao contrário dos juros simples — onde os rendimentos são obtidos mas não reinvestidos —, os juros compostos distinguem-se por:

• Efeito multiplicador: Os juros compostos têm um efeito multiplicador, uma vez que os juros obtidos sobre o capital inicial permanecem investidos. Assim, a rentabilidade passa a incidir sobre um montante crescente, e cada novo período gera rendimentos superiores aos anteriores.
• Crescimento do capital investido: Nos juros simples, os ganhos são resgatados periodicamente, mantendo-se inalterado o capital investido. Com os juros compostos, as receitas permanecem investidas, fazendo com que o capital total aumente ao longo do tempo.

Leia também ➡️ Juros simples vs juros compostos

Quais são os benefícios dos juros compostos?

Os juros compostos beneficiam o investidor por permitirem um crescimento mais rápido do capital do que os juros simples. Mas essa não é a sua única vantagem.

Além de proporcionarem uma valorização contínua e acelerada, os juros compostos adaptam-se a qualquer perfil de investidor. Ou seja, não é necessário ser um especialista nem escolher ativos complexos para tirar partido deste efeito.

Quer seja um investidor profissional ou alguém que está apenas a começar a aplicar o seu dinheiro, a regra principal dos juros compostos é simples: reinvestir os ganhos. E se, além disso, fizer reforços regulares através de uma estratégia DCA (Dollar Cost Averaging), o crescimento do seu património será ainda mais expressivo.

Em poucos anos, poderá reunir um montante significativo em investimentos — quaisquer que sejam os seus objetivos financeiros.

Fórmula e cálculo dos juros compostos

Já vimos o que são os juros compostos, mas como se calculam, na prática? Vamos explicar a fórmula e depois ver alguns exemplos reais — com e sem reforços mensais.

Os juros compostos funcionam através da aplicação de uma taxa de juro não só sobre o capital inicial, mas também sobre os juros que esse capital vai acumulando ao longo do tempo. Esta característica dá origem ao famoso efeito “bola de neve”.

Embora o cálculo dos juros compostos pode parecer complexo à primeira vista, mas com uma fórmula simples é possível estimar com precisão o crescimento de um investimento.

Elementos da fórmula

A fórmula tradicional dos juros compostos é a seguinte:

M = C × (1 + i)^n

Onde:

• M é o montante final acumulado
• C é o capital inicial investido
• i é a taxa de juro por período (em formato decimal, por exemplo, 7% = 0,07)
• n é o número total de períodos (anos, meses, etc.)

Se forem feitos aportes regulares, como contribuições mensais, a fórmula é ajustada para refletir esse reforço contínuo:

M = C × (1 + i)^n + R × [((1 + i)^n – 1) / i]

Onde:

• R é o valor do reforço periódico (mensal, trimestral, etc.)

Exemplo prático de juros compostos

Imagina que investes 1.000 € com uma rentabilidade anual de 7%. Isso significa que, todos os anos, ganharias 70 € de rendimento. Se optares por juros simples, retirarias esses 70 € no final de cada ano e manterias o capital inicial de 1.000 €, voltando a ganhar sempre os mesmos 70 € por ano. Ao fim de 10 anos, terias acumulado 700 € de rendimento.

Se, por outro lado, optares por juros compostos, esses 70 € que ganhas no primeiro ano são reinvestidos. No segundo ano, os 7% passam a aplicar-se sobre 1.070 €, o que gera 74,90 € de juro, e assim sucessivamente. Ao final de 10 anos, terias acumulado 967,12 € em juros — ou seja, praticamente duplicarias o capital inicial.

Investimento inicial	Juro anual	Rendibilidade (10 anos, juro simples)	Rendibilidade (10 anos, juro composto)
1.000 €	7%	700 €	967,12 €

Só com este exemplo, já se percebe bem o impacto que os juros compostos podem ter num investimento. E repara: falamos apenas de aplicar 1.000 €, sem fazer reforços adicionais.

Agora vejamos um segundo exemplo com uma estratégia de DCA (Dollar Cost Averaging), ou seja, com aportes mensais.

 Como os aportes mensais afetam os juros compostos? 

Imagina que, além do investimento inicial de 1.000 €, aplicas 50 € por mês (o que equivale a 600 € por ano), mantendo a mesma taxa de juro de 7% ao ano.

Neste cenário, ao fim de 10 anos terias acumulado 10.257 €.

Se, em vez disso, tivesses apenas poupado esse valor sem investir, terias juntado 7.000 € no mesmo período (1.000 € + 600 € x 10 anos).

Este segundo exemplo mostra ainda melhor como os juros compostos, combinados com disciplina de poupança regular, podem acelerar significativamente o crescimento do teu capital.

Simulação com a nossa calculadora de juros compostos

E, felizmente, graças à tecnologia, já não precisamos de fazer estes cálculos manualmente — existem hoje inúmeras calculadoras de juros compostos online, onde basta introduzir os parâmetros relevantes.

Na prática, estas ferramentas utilizam a mesma fórmula que explicámos no ponto anterior, mas fazem os cálculos de forma automática, poupando-lhe tempo e esforço.

Vamos mostrar-lhe como utilizar a nossa própria calculadora de juros compostos.

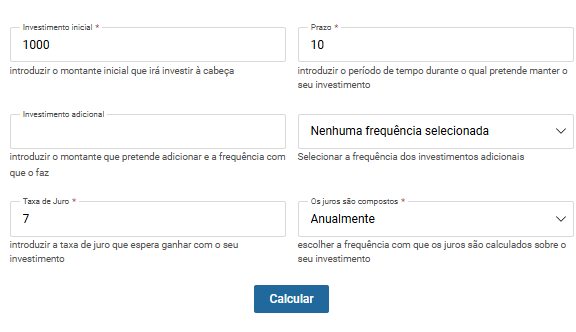
Parâmetros usados na simulação:

• Investimento inicial: 1.000€
• Investimento adicional: Nenhum
• Prazo: 10 anos
• Taxa de juro: 7% ao ano
• Capitalização: Anual

Com estes dados, basta clicar no botão “Calcular” e o resultado será exibido automaticamente. O montante final obtido com juros compostos anuais será de: 1.967,15 €

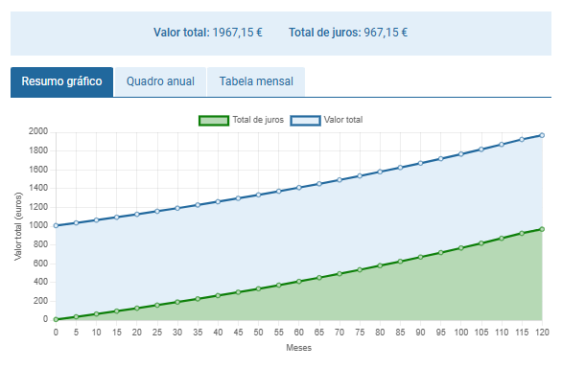
Assim, na tabela seguinte pode ver o exemplo do ponto anterior detalhado ano a ano, o que permite compreender melhor como se realiza o cálculo dos juros compostos.

Ano	Montante acumulado (€)	Juros do ano (€)
1	1.070,00	70,00
2	1.144,90	74,90
3	1.225,04	80,14
4	1.310,79	85,75
5	1.402,54	91,75
6	1.500,71	98,17
7	1.605,76	105,05
8	1.718,16	112,40
9	1.838,43	120,27
10	1.967,15	128,69

Juros compostos semestrais

Para calcular os juros compostos semestrais, é necessário aplicar a taxa de juro a cada seis meses.
É bastante simples: basta dividir a taxa anual — neste exemplo, 7% — por 2, o que resulta numa taxa semestral de 3,5%.

Assim, no primeiro semestre, com um investimento inicial de 1.000 euros, os juros seriam de 35 €.

Juros compostos mensais

No caso dos juros compostos mensais, o processo é idêntico: dividimos a taxa anual de 7% por 12 meses, obtendo uma taxa mensal de aproximadamente 0,58%. Isto significa que, no primeiro mês, o juro gerado sobre os 1.000 euros investidos seria de 5,80 €.

Juros compostos diários

Considerando que um ano (exceto os bissextos) tem 365 dias, devemos dividir a taxa anual de 7% por 365, resultando numa taxa diária de aproximadamente 0,019%. Ou seja, no primeiro dia, com um investimento de 1.000 euros, o juro acumulado seria de 0,19 €.

Como se pode ver, calcular os juros compostos é relativamente simples, mas pode tornar-se moroso se pretender simular vários anos ou diferentes periodicidades (diária, mensal, trimestral, etc.).

Por essa razão, existem hoje várias calculadoras de juros compostos online que facilitam este processo.
A nossa calculadora, por exemplo, permite não só simular diferentes cenários com várias frequências de capitalização, como também enviar os resultados diretamente para o seu e-mail.

Um exemplo da força dos juros compostos: como se explica a fortuna de Warren Buffett?

Warren Buffett é um investidor de referência, considerado por muitos como o melhor da história, por ter conseguido, através das suas decisões de investimento, superar de forma consistente o desempenho médio do mercado bolsista.

Quando questionado sobre o segredo do seu sucesso, Buffett costuma dizer que, ao longo das suas seis décadas como investidor, o seu maior aliado foi o juro composto. Ou seja, reinvestir os lucros obtidos permitiu-lhe tornar-se um dos homens mais ricos do mundo, fazendo crescer o seu património com uma estratégia simples, mas extremamente eficaz.

Para compreender melhor a magnitude deste fenómeno e a forma como o chamado “Oráculo de Omaha” o aproveitou, é preciso recuar até aos seus primeiros passos. Buffett começou a investir com apenas 11 anos, quando comprou a sua primeira ação por 38 dólares. Nove anos depois, ainda muito jovem, já tinha poupado cerca de 10.000 dólares. Com o passar do tempo, viria a adquirir uma pequena empresa têxtil chamada Berkshire Hathaway por 7.500 dólares.

No entanto, é aqui que entra a verdadeira “magia”: 99% da fortuna de Buffett foi acumulada depois dos 65 anos, quando o efeito multiplicador dos juros compostos se manifestou em toda a sua força.

Na verdade, é possível observar como o seu património se tornou cada vez mais avultado — especialmente nos últimos anos. E não é (apenas) porque, já nonagenário, seja melhor investidor do que era antes. O que explica esse crescimento é o facto de ter conseguido gerar e reinvestir somas significativas de capital, que, por sua vez, passaram a gerar montantes ainda mais expressivos de rendimento.

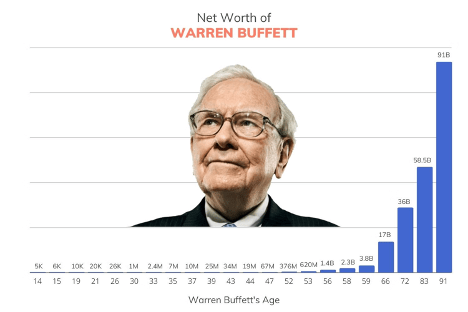
Graças à consistência e ao poder dos juros compostos, a fortuna atual de Warren Buffett ultrapassa os 135 mil milhões de dólares.

Onde investir para beneficiar do efeito dos juros compostos Portugal

Agora que provavelmente já compreende melhor como funcionam os juros compostos, é o momento ideal para explorar algumas ideias de investimento que permitem tirar o máximo partido deste efeito.

É importante ter em conta que, nos exemplos que apresentámos anteriormente, a taxa de juro composta é considerada fixa ao longo dos anos — o que raramente acontece na realidade. No mundo dos investimentos, as taxas de juro variam consoante o desempenho dos ativos nos quais se investe.

A seguir, apresentamos várias opções para investir com juros compostos:

Corrtoras que pagam juros sobre capital não investido

Algumas corretoras remuneram o saldo disponível na conta de investimento que ainda não foi aplicado. Esse valor gera juros que são capitalizados com frequência (diária ou mensal), permitindo obter rendimentos passivos e tirar partido do efeito dos juros compostos.

Trading 212

A Trading 212 é uma corretora europeia conhecida pela sua plataforma intuitiva e zero comissões em ações e ETFs. Além disso, oferece uma das contas remuneradas mais generosas do mercado, com juros diários sobre o saldo não investido em até 13 moedas diferentes.

• Montante mínimo/máximo: sem limites
• Pagamento de juros: diário
• Remuneração:
  • Dólares: 4,1%
  • Euros: 3%

Nota: Os juros aplicam-se apenas sobre o saldo em conta de investimento. Aplicam-se termos. O capital investido está sujeito a risco.

XTB

A XTB é uma corretora bem estabelecida e regulada, com uma forte presença em Portugal. Desde 2023, passou a remunerar os fundos não investidos, com condições diferenciadas para novos e antigos clientes. Oferece ainda ações e ETFs sem comissões até 100.000€/mês.

• Montante mínimo/máximo: sem limites
• Taxas de juro:
  • Novos clientes: até 2,8% (EUR) e 4,2% (USD)
  • Clientes existentes: até 1,15% (EUR) e 2,1% (USD)
• Pagamento de juros: mensal (com cálculo diário)

Interactive Brokers

Uma das corretoras mais completas do mundo, ideal para investidores experientes. A IBKR oferece remuneração sobre fundos não investidos em múltiplas moedas, com acesso a uma enorme variedade de mercados globais. No entanto, para aceder à taxa máxima de juro, é necessário cumprir certos requisitos de saldo mínimo.

• Taxas de juro:
  • 4,2% (USD)
  • 2,1% (EUR)
• Requer depósito mínimo de 10.000 USD para obter a taxa máxima
• Pagamento de juros: mensal

Fundos de investimento e ETFs

Os fundos de investimento reúnem o capital de vários investidores, sendo geridos por profissionais que aplicam esse montante em diferentes ativos. A grande vantagem é a diversidade: existem fundos de obrigações, ações, mistos, indexados, entre outros.

Os fundos indexados, por exemplo, replicam o desempenho de um índice bolsista, como o S&P 500 ou o IBEX35. Compram participações nas empresas que compõem esses índices e acompanham a sua valorização ou desvalorização.

Como a economia tende a crescer no longo prazo, os fundos indexados são uma excelente forma de beneficiar do juro composto.

Outra opção são os ETFs (fundos cotados em bolsa), que funcionam de forma semelhante, mas com a diferença de que são negociados em tempo real no mercado.
A principal vantagem dos fundos tradicionais face aos ETFs é que podem ser transferidos entre si sem gerar tributação imediata, enquanto os ETFs obrigam à declaração anual de ganhos.

👉 Encontre também os melhores fundos de investimento.

Dicas de investimento por montante disponível

O juro composto pode ser aplicado a qualquer valor — desde pequenas poupanças mensais até grandes patrimónios. Veja os nossos guias específicos para saber onde investir consoante o seu capital disponível:

• Onde investir com pouco dinheiro
• Onde investir 5.000 euros
• Onde investir 20.000 euros
• Onde investir 100.000 euros
• Onde investir em Portugal

Qualquer que seja o valor, o importante é começar e manter uma estratégia disciplinada de reforços e reinvestimento dos ganhos.

Porque é tão importante o juro composto nos investimentos?

O juro composto é extremamente importante nos investimentos por várias razões. A mais evidente é que permite que o seu dinheiro cresça mais rapidamente, o que está alinhado com o objetivo de qualquer investidor: aumentar o capital ou, no mínimo, rentabilizar o património existente.

Mas o juro composto destaca-se também pela sua versatilidade — como referimos anteriormente, adapta-se a qualquer estratégia de investimento.
Independentemente dos produtos escolhidos, o juro composto será sempre um aliado poderoso para melhorar a rentabilidade no longo prazo.

Quando se notam mais os efeitos do juro composto?

Tal como vimos, o maior aliado do juro composto é o tempo. Ou seja, quanto mais longo for o horizonte do investimento, mais evidentes serão os seus efeitos.

Além disso, uma estratégia que potencia significativamente os benefícios do juro composto é a realização de reforços periódicos. Esta prática permite fazer crescer o património a dobrar — algo bem visível no exemplo prático que apresentámos anteriormente.

Vantagens e riscos do juro composto

As principais vantagens do juro composto são:

• Permite que o seu capital cresça mais rapidamente
• Adapta-se a qualquer tipo de investimento

Já no que diz respeito aos riscos, é importante referir que o juro composto, por si só, não implica risco de perda de capital. O risco está associado ao produto financeiro em que se investe, uma vez que todos os investimentos envolvem possibilidade de ganhos ou perdas.

No entanto, há um risco potencial a considerar: o de perder oportunidades de rentabilidade superior por manter o capital numa aplicação com retorno mais conservador.

Exemplo: se reinvestir os seus lucros numa aplicação que gera 7% ao ano, poderá estar a perder a oportunidade de aplicar esse valor num produto com maior potencial de rentabilidade (ainda que com maior risco).

Como em qualquer decisão de investimento, é essencial analisar bem o mercado, compreender o seu perfil de investidor e definir o montante que está disposto a arriscar.

Agora que já sabe o que é o juro composto, como se calcula e onde investir para tirar partido dele, chegou a sua vez:

Vai continuar a investir em empresas do mercado de forma ativa, ou considera optar por uma estratégia mais passiva, mas com maior segurança a longo prazo?

FAQs

Este artigo é meramente informativo e educacional. As informações fornecidas aqui não podem ser consideradas como aconselhamento financeiro ou recomendação de compra / venda.